На Главную

ГДЗ: Английский язык       Алгебра       Геометрия       Физика       Химия       Русский язык       Немецкий язык

Подготовка к экзаменам (ЕГЭ)       Программы и пособия       Краткое содержание       Онлайн учебники
Шпаргалки       Рефераты       Сочинения       Энциклопедии       Топики с переводами

Учебник по Тригонометрии.


Оглавление учебника


ТРИГОНОМЕТРИЯ

9. Свойства тригонометрических функций у = tg x и у = ctg x и их графики.

Так же, как при обосновании свойств синуса и косинуса заменим х на a .

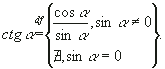
  1. D[tg] - любое a О R : a № p/2 + pk,

    2. D[сtg] - любое a О R : a № pk,

    k =0, ± 1, ± 2, … .

  2. E[tg] = E[ctg] - (-Ґ , +Ґ ).

Оси тангенсов и котангенсов являются касательными к единичной окружности в точках А и В соответственно и обладают аналогичными свойствами числовых прямых, что и оси Оу и Ох соответственно в том смысле , что положительное и отрицательное направления на оси тангенсов (котангенсов) совпадают с положительным и отрицательным направлениями оси Оу (Ох); единицы измерения на них те же, что и на всей координатной плоскости, в том числе и на осях Оу и Ох; начала отсчета на оси тангенсов - точка А (1; 0); а на оси котангенсов - точка В (0; 1).

Фиксируем произвольные числа а0, b0 О R, а0 « М', b0 « М', на осях тангенсов и котангенсов соответственно. М' « М на правой и соответственно верхней полуокружностях, М - М (x; y); М « a0 О (-p/2, p/2), соответственно М « b0 О (0, p); tg a0 = а0, соответственно tg b0 = b0.

Докажем последние два равенства.

При a0 № 0 прямоугольные треугольники ОММх и ОМ'А подобны как имеющие общий острый угол, следовательно,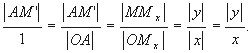

Последнее равенство выполняется в силу того, что x > 0. Так как знаки величин отрезков АМ ' и МхМ совпадают, то и имеют место равенства

Если a0 = 0, то точки М, М' и А совпадают, а потому и в этом случае также а0 = АМ' = 0 = tg 0 = tg a0. По определению a0 = arctg а0.

Соответственно при b0 № p/2 прямоугольные треугольники ОММу и ОМ'В подобны как имеющие общий острый угол, следовательно,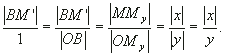

Последнее равенство выполняется в силу того, что у > 0. Так как знаки величин отрезков ВМ 'и МуМ совпадают, то и имеют место равенства

Если b0 = p/2, то точки М, М' и В совпадают, а потому и в этом случае также b0 = BМ' = 0 = ctg p/2 = ctg b0. По определению b0 = arcctg b0.

III. В силу результатов п. II ясно, что функции тангенс и котангенс не имеют наибольшего и наименьшего значений на своих областях определения.

IV. При исследовании четности или нечетности функций тангенс и котангенс (согласно определению этих свойств) сначала докажем, что для любого a О D[tg] или a О D[сtg], то есть "n О Z a № p/2 + pn, соответственно "m О Z a № pm -a также принадлежит соответствующей области определения.

Предположим, что при некотором a из области определения тангенса или котангенса -a в эту область не входит, тогда мы получим, что -a = p/2 + pn', n' О Z, соответственно -a = pт', т' О Z. Откуда a = -p/2 - pn' = p/2 - p (n' + 1) = p/2 + pn0, где n0 = -(n' + 1) О Z, соответственно a = -pт' = p (-т' ) = pт0, где т0 = -т' О Z. Получили противоречие. Следовательно, "n О Z -a № p/2 + pn, соответственно "m О Z -a № pm, то есть области определения функций тангенс и котангенс симметричны относительно начала координат.

Далее нечетность функций тангенс и котангенс уже непосредственно вытекает из их определений, нечетности синуса и четности косинуса следующим образом:

"a О D[tg]

"a О D[сtg]

 

  1. При исследовании периодичности функций тангенс и котангенс (согласно определению этого свойства) сначала установим, что если a О D[tg] или a О D[сtg], то "т О Z a + pт О D[tg], соответственно a + pт О D[сtg].

    2. Предположим, что при некотором a из области определения тангенса или котангенса и некотором целом значении т' a + pт' в эту область не входит, тогда мы получим, что a + pт' = p/2 + pn', n' О Z, соответственно a + pт' = pn', n' О Z. Отсюда вытекает, что a = p/2 + pn' - pт'= p/2 + p (n' - т') = p/2 + pn0, где n0 = n' - т' О Z, соответственно a = pn' - pт' = p (n' - т' ) = pт0, где т0 = n' - т' О Z. Следовательно, указанное значение a не входит в область определения тангенса или соответственно котангенса. Получили противоречие, которое доказывает сформулированное выше утверждение.

    Далее периодичность тангенса и котангенса вытекает следующим образом:

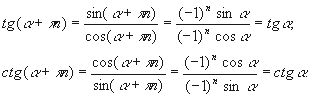
    при любом a из области определения тангенса или котангенса и любом целом значении n. А это и означает периодичность каждой из этих функций с периодами pn, n = ± 1, ± 2, … .

  2. Из результатов п. VI исследования функций синус и косинус и определений функций тангенс и котангенс вытекает, что

    3. tg a = 0 Ы sin a = 0 Ы a = pn,

    сtg a = 0 Ы соs a = 0 Ы a = p/2 + pn,

    n = 0, ± 1, ± 2, … .

    tg a и сtg a положительны (отрицательны) тогда и только тогда, когда функции синус и косинус принимают значения одного знака (разных знаков). Следовательно, функции тангенс и котангенс положительны на каждом из интервалов (pn; p/2 + pn) и отрицательны на каждом из интервалов (-p/2 + pn; pn) "n О Z.

  3. Функция тангенс возрастает на (-p/2 + pn, p/2 + pn) "n О Z, причем на каждом из этих интервалов в отдельности, а функция котангенс убывает на (pn, p + pn) "n О Z и также на каждом из этих интервалов в отдельности.

    4. Доказательства. В силу периодичности этих функций и утверждения 2, доказанного во "Введении", достаточно доказать эти утверждения для случая n = 0. Фиксируем произвольные х1 и х2, где -p/2 < х1< х2 < p/2 в случае тангенса, и 0 < х1 < х2 < p в случае котангенса, откуда в силу свойств числовых неравенств в обоих случаях 0 < х2 - х1 < p. Применим формулы разностей тангенсов и котангенсов аргументов х2 и х1:

    Первая из этих формул доказана выше (Глава 3, формула (7) для знака "-"), а вторая доказывается аналогично указанной формуле следующим образом:

    В силу результатов исследования п. VI о промежутках знакопостоянства функций синус и косинус, мы и получаем, что

    tg х2 - tg х1 > 0 ; tg х2 - tg х1 < 0.

    Отсюда и вытекают доказываемые утверждения.

  4. Графики.

   

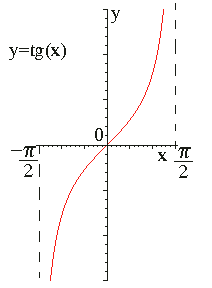
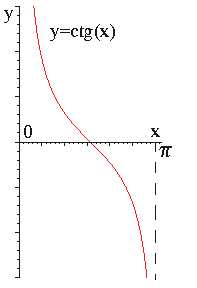
 Отметим, что при

  а при