Учебник по Геометрии.

Оглавление учебника

ГЕОМЕТРИЯ: Планиметрия

7. Окружность

Форма и положение окружности.

Теорема. Через три точки, не лежащие на одной прямой можно провести окружность и притом только одну.

Теорема. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.

Следствия.

1. Диаметр, проведённый через середину хорды, перпендикулярен этой хорде и делит дугу, стягиваемую ею, пополам.

2. Диаметр, проведённый через середину дуги, перпендикулярен хорде, стягивающей эту дугу, и делит её пополам.

Теорема. Дуги, заключённые между параллельными хордами равны.

Зависимость между дугами и хордами.

Теоремы. В одном круге ( или равных кругах) :

1) если дуги равны, то стягивающие их хорды равны,

2) если хорды равны, то стягиваемые ими дуги равны.

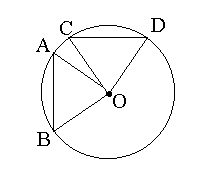
Доказательство. 1) Пусть дуга АВ равна дуге CD . Проведя радиусы ОА, ОВ, ОС и OD, мы получим,два треугольника, у которых две стороны одного равны двум сторонам другого и углы между ними равны. Следовательно, эти треугольники равны и AB=CD. 2) Если хорды АВ и CD равны, треугольники АОВ и COD равны, имея три соответственно равные стороны, а потому РAOB=Р COD. Если же центральные углы равны, то и соответствующие им дуги равны.

Теоремы. В одном круге ( или равных кругах) :

1) если хорды равны, то они одинаково удалены от центра,

2) если хорды одинаково удалены от центра, то они равны.

Относительное положение прямой и окружности. Прямая и окружность могут находиться только в трёх относительных положениях.

1. Расстояние от центра до прямой больше радиуса окружности.

2. Расстояние от центра до прямой меньше радиуса окружности.

3. Расстояние от центра до прямой равно радиусу окружности.

В третьем случае прямая имеет с окружностью только одну общую точку, такая прямая называется касательной к окружности, общая точка называется тогда точкой касания.

1. Если прямая перпендикулярна радиусу в конце его, лежащем на окружности, то она касается окружности.

2. Если прямая касается окружности, то радиус, проведённый в точку касания перпендикулярен прямой.

Следствие. Две касательные, проведённые из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей точку с центром .

Относительное положение двух окружностей. Если две окружности имеют только одну общую точку, то говорят, что они касаются, если же две окружности имеют две общие точки, то говорят, что они пересекаются. Будем называть линией центров прямую, проходящую через центры двух окружностей.

Теорема. Если две окружности имеют общую точку, расположенную вне линии центров, то они имеют ещё и другую общую точку, симметричную с первой относительно линии центров.

Теорема.

1. Если две окружности имеют общую точку на линии их центров, то они касаются.

2. Если две окружности касаются, то точка качания лежит на линии центров.

Вписанный угол. Угол, образованный двумя хордами, исходящими из одной точки окружности, называется вписанным углом.

Теорема. Вписанный угол измеряется половиной дуги, на которую опирается.

Следствия. 1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой.

2. Всякий угол, опирающийся на диаметр, есть прямой.

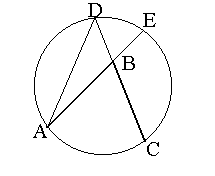
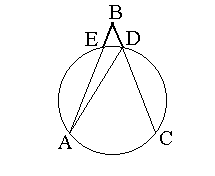
Теоремы. 1. Угол, вершина которого лежит внутри круга измеряется полусуммой двух дуг, одна из которых заключена между его сторонами, а другая - между продолжениями сторон.

2. Угол , вершина которого лежит вне круга и стороны которого пересекаются с окружностью, измеряется полуразностью двух дуг, заключённых между его сторонами.

 

Доказательство. Проведя хорду AD мы получим треугольник ,относительно которого рассматриваемый угол АВС служит внешним , когда его вершина лежит внутри круга, внутренним, когда его вершина лежит вне круга. Поэтому:

в первом случае: РABC=РADC+РDAE,

во втором случае: РABC=РADC-РDAE.

Но углы ADC и DAE , как вписанные измеряются половинами дуг AC и DE ,следовательно, теорема доказана.

Вписанные и описанные многоугольники. Если все вершины многоугольника лежат на окружности, то говорят, что этот многоугольник вписан в окружность или что окружность описана около него.

Если все стороны многоугольника касаются окружности, то говорят, что многоугольник описан около окружности или что окружность вписана в треугольник.

Теоремы. 1. Около всякого треугольника можно описать окружность и только одну.

2. Во всякий треугольник можно вписать окружность и только одну.

Свойство вписанного четырёхугольника: В выпуклом вписанном четырёхугольнике сумма противоположных углов равна двум прямым. Обратно, если в выпуклом четырёхугольнике сумма противоположных углов равна двум прямым, то около него можно описать окружность.

Следствия. 1. Из всех параллелограммов только около прямоугольника можно описать окружность.

2. Около трапеции можно описать окружность только тогда, когда она равнобочная.

Свойство описанного четырёхугольника: В описанном четырёхугольнике суммы противоположных сторон равны.

Четыре замечательные точки в треугольнике.

1. Три перпендикуляра к сторонам треугольника, проведённые через их середины, сходятся в одной точке, которая есть центр описанного круга.

2. Биссектрисы углов треугольников сходятся в одной точке, которая есть центр вписанного круга.

3. Три высоты треугольника пересекаются в одной точке.

4. Три медианы треугольника пересекаются в одной точке, эта точка отсекает от каждой медианы третью часть, считая от соответствующей стороны.