Учебник по Математике и Алгебре.

Оглавление учебника

АЛГЕБРА: Неравенства

6.3. Дополнительные неравенства

Неравенство, связывающее среднее арифметическое и среднее геометрическое двух чисел.

Пусть даны два числа a, b О R . Число называется их средним арифметическим.

Пусть a, b О R, a і 0 и b і 0. Число называется их средним геометрическим.

Теорема 9.

Пусть a, b О R : a і 0 и b і 0

(1)

причем " і " обращается в " = " Ы a = b.

Доказательство. Достаточно показать, что

(2)

Преобразуя левую часть неравенства (2), получаем

,

очевидно. Из последнего неравенства уже ясно, что в неравенстве (1) имеет место равенство в том и только в том случае, когда .

Дополнительные вопросы: доказать неравенства

, ,

где a, b, c, d і 0 (первое вытекает из теоремы 9 : , где , , а второе следует из первого при ).

Неравенство для суммы двух взаимно обратных чисел.

Пусть число a № 0. Число называется обратным к числу a.

Так как , то a - число, обратное числу , следовательно, числа a и 1/a - взаимно обратные.

Теорема 10.

Пусть a № 0, тогда,

если a > 0, то , (3)

если a < 0, то , (4)

причем неравенства обращаются в равенства тогда и только тогда, когда соответственно a = 1, a = -1.

Доказательство. В случае a > 0, справедливость неравенства (3) сразу вытекает из (1) при , а так как в данном случае a = b Ы a = 1, то в случае a > 0 теорема доказана.

В случае a < 0 можно воспользоваться доказанной первой частью теоремы применительно к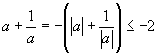 , из которой вытекает , а так как в этом случае только при a = -1, теорема доказана и для этого случая.