На Главную

ГДЗ: Английский язык       Алгебра       Геометрия       Физика       Химия       Русский язык       Немецкий язык

Подготовка к экзаменам (ЕГЭ)       Программы и пособия       Краткое содержание       Онлайн учебники
Шпаргалки       Рефераты       Сочинения       Энциклопедии       Топики с переводами

Учебник по Математике и Алгебре.


Оглавление учебника


АЛГЕБРА: Графики функций

5.5. Свойства степенной функции с целым показателем и ее график

Функция вида y = f(x) = xn , где хО R - переменная, n О Z - постоянное число, называется степенной функцией с целым показателем.

n = 1 - это частный случай линейной функции, а n = 2 - частный случай квадратичной функции. При n = 0 " х № 0 f(x) = 1, f (0) не определено.

  1. Случай n і 3.
  1. D[xn] - (-Ґ, +Ґ ), так как "x О R определено однозначно число xn , как произведение n чисел, каждое из которых равно x.
  2. Е[xn] - (-Ґ, +Ґ ), если n = 2k -1, k і 2, kО N ;

Е[xn] - [0, +Ґ ), если n = 2k, k і 2, kО N ;

Доказательство. " nО N ; " y0 і 0 существует единственное х0 і 0 :

, ;

в то же время при n = 2k из свойств операции умножения действительных чисел следует, что "x О R xn = x2k і 0;

При n = 2k -1 " y0 < 0 существует :

.

III. Если n = 2k , то существует , так как "x О R xn і 0, не существует , что легко доказывается от противного на основе результатов пункта II.; Если же n = 2k - 1, то из пункта II. вытекает (также от противного) отсутствие наибольшего и наименьшего значений у функции y = xn ,на всей ее области определения.

IV. D[xn] - R симметрична относительно точки х0 = 0. Если n = 2k , то"x О R, ( -х)n=(-1)nЧ хn = хn , то есть "x О R, f(- х) = f( х), следовательно функция четная.

Если же n = 2k -1, то"x О R, ( -х)n=(-1)nЧ хn = - хn , то есть "x О R, f(- х) = -f( х), следовательно функция нечетная.

V. Функция y = xn "n О N , не периодическая, так как она строго монотонна на бесконечных промежутках. (см. далее п. VII).

VI. Из свойств операции умножения действительных чисел вытекает: если n = 2k , то f(x) = xn > 0 на интервалах (-Ґ , 0) и (0, +Ґ ); а если n = 2k - 1, то f(x) = xn > 0 на интервалах (0, +Ґ ) и f(x) = xn < 0 на интервалах (-Ґ , 0). Так как "n О N , при x = 0 xn = 0, то х0 = 0 - единственный нуль функции.

VII. Пусть x1, x2 - произвольные числа из R , удовлетворяющие неравенствам 0 Ј x1 < x2 , тогда "n О N в силу свойств числовых неравенств вытекает x1n < x2n , следовательно функция y = xn возрастает на промежутке [0, +Ґ ).

Пусть теперь x1, x2 - произвольные числа из R , удовлетворяющие неравенствам -x1 < -x2 Ј 0 Ы 0 Ј x2 < x1 , тогда при n = 2k в силу четности функции и свойств неравенств (-x1)n = -x1n < -x2n = (-x2)n , следовательно функция y = xn убывает на промежутке (-Ґ, 0];

При n = 2k - 1 в силу нечетности функции и свойств неравенств (-x1)n = -x1n < -x2n = (-x2)n , следовательно функция y = xn возрастает на промежутке (-Ґ, 0 ], а так как она возрастает и на промежутке и на промежутке [0, +Ґ ), то она будет возрастающей на всей числовой прямой (-Ґ, +Ґ ).

VIII. Графики функций

 

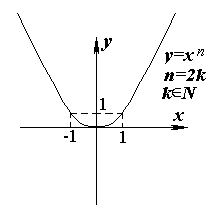
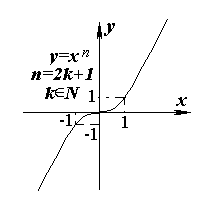
О(0; 0) - точка пересечения графика функции y = xn с осями Ох и Оу.

 

  1. Случай n Ј -1.

Положим n = -т, где уже т О N.

I. D[xn] = D[x -т]- (-Ґ, 0) И (0, +Ґ ), так как " х № 0 x т № 0, а потомуопределено, но при х = 0 x т = 0, поэтому xn =1/ x т не определено.

II. Е[xn] = Е[x -т]- (0, +Ґ ), если n = -2k, kО N ;

Е[xn] = Е[x -т]- (-Ґ, 0) И (0, +Ґ ), если n = -(2k - 1), kО N . Этот случай доказывается аналогично случаю натурального значения n , отметим только, что так как " х № 0 1/x т № 0, а потому y0 = 0 П Е[xn].

III. Таким же образом, как и в случае натурального n из пункта II. вытекает несуществование при n = -(2k - 1) и при любом n Ј -1. Подробнее остановимся на доказательстве несуществования

при n = -2k . Если предположить его существование, то он будет равен некоторому числу т > 0. А согласно результатам пункта II, в частности для числа т/2 существует х0'і 0: f( х0') = m/2 = < m , пришли к противоречию.

IV., V. Эти случаи полностью аналогичны случаю nО N.

VI. Из п. II вытекает, что нулей функция не имеет, а интервалы знакопостоянства у нее такие же (в зависимости от четности и нечетности n ), что и в случаи натурального показателя n.

VII. Функция y = xn убывает на промежутке (0, +Ґ ) при любом n Ј -1, а также она убывает на промежутке (-Ґ , 0) при n = -(2k - 1) и возрастает на этом промежутке при n = -2k.

Для доказательства фиксируем произвольные 0 < x1 < x2 , так как при этом 0 < x1m < x2m , то в силу свойств числовых неравенств .

Далее, рассматривая произвольные числа x1, x2 , удовлетворяющие неравенствам -x1 < -x2 Ј 0 Ы 0 Ј x2 < x1 , совершенно аналогично случаю натурального показателя n на основе четности или нечетности функции y = xn и свойств числовых неравенств доказывается, что (-x1)n < (-x2)n при n = -2k и (-x1)n > (-x2)n при n = -(2k - 1).

Замечание. Необходимо отметить, что при n = -(2k - 1) убывания функции y = xn на объединении промежутков (-Ґ, 0) И (0, +Ґ ) нет! Если, к примеру, x1 < 0 < x2 , то есть x1 < x2 , то также x1n < 0 < x2n , то есть x1n < x2n.

VIII. Графики функций

 

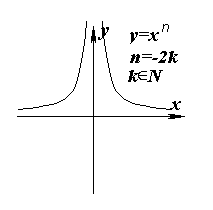
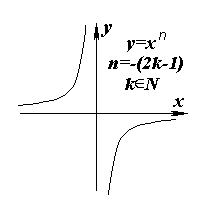
 Отметим, что так как число 0 не принадлежит ни к области определения, ни к области значений функции y = xn в рассматриваемом случае, графики этих функций не имеют точек пересечения с осями координат. При n Ј -1

Если n = -2k , то при х ® ± Ґ ( х ® 0 ± 0) f(x) ® 0 + 0 (f(x) ® + Ґ ).

Если n = -(2k - 1), то при х ® ± Ґ ( х ® 0 ± 0) f(x) ® 0 ± 0 (f(x) ® ± Ґ ).

Замечание. По определению кривые, являющиеся графиками функций y = xn при n = 2 и n = -1, называются соответственно параболой и гиперболой.