Учебник по Математике и Алгебре.
Оглавление учебника
АЛГЕБРА: Числа
2.5. Арифметические корни n - ой степени и степени с рацоинальными показателями
Свойства арифметических корней
n - ой степени.Пусть числа
a, b О R. Число b называется корнем n - ой степени (n О N) из числа а (алгебраическим корнем), если![]() .
.
Это обозначение применяется и для случая нечетного
n и отрицательного а ( а<0), при этом также b<0.При
n = 1 b = a , так какБез доказательства принимается существование арифметического корня
n - ой степени; его единственность вытекает из свойства 10 числовых неравенств.Свойства корней
n - ой степени: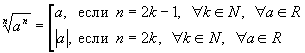
![]() , " n, m, k, r О N, m = nk + r, 0 < r Ј n-1, " a і 0, a О R
, " n, m, k, r О N, m = nk + r, 0 < r Ј n-1, " a і 0, a О R
6. ![]() , " n, m О N, " a і 0, a О R
, " n, m О N, " a і 0, a О R
7. ![]() , " n, m, p, q, k О N, m = kq, n = kp, " a і 0, a О R
, " n, m, p, q, k О N, m = kq, n = kp, " a і 0, a О R
8. ![]() , " n, m, p, q О N, " a і 0, a О R
, " n, m, p, q О N, " a і 0, a О R
![]() , " n, m, p, q О N, " a і 0, a О R.
, " n, m, p, q О N, " a і 0, a О R.
Доказательства.
Их доказательства основаны на определении корня, единственности корня (в свойстве 1. применяется еще единственность алгебраического корня нечетной степени из отрицательного числа) и свойствах степеней с натуральными показателями.
1. ![]() и
и ![]() Ю
Ю ![]() , n = 2k
-1, если n = 2k
, то так как
, n = 2k
-1, если n = 2k
, то так как ![]() " nОN
" nОN ![]() , что выводится точно так же, как и в случае n = 2k
-1 (при этом используется то, что
, что выводится точно так же, как и в случае n = 2k
-1 (при этом используется то, что ![]() );
);
2. ![]() ,
, ![]() Ю 2.;
Ю 2.;
3. 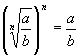 ,
, 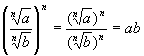 Ю 3.;
Ю 3.;
4. ![]() ,
, ![]() Ю 4.;
Ю 4.;
5. ![]() ,
, ![]() Ю 5.;
Ю 5.;
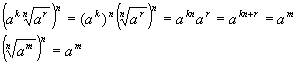 Ю 5.;
Ю 5.;
6. 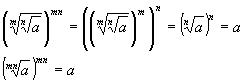 Ю 6.;
Ю 6.;
7.![]()
![]() ;
;
8.![]()
![]() , аналогично рассматривается случай частного с использованием свойства 4. степеней.
, аналогично рассматривается случай частного с использованием свойства 4. степеней.
Свойства корней полностью доказаны.
Обратить внимание, что в свойствах 2 и 3 при n = 2k, kОN для любых a,b О R таких, что ab і 0 (в случае 3 b № 0) имеют место равенства, которые предлагается самостоятельно обосновать.
2'. ![]() и 3'.
и 3'. 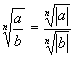 .
.
Свойства степеней с рациональными показателями.
Пусть
p О Z, q О N, a > 0, a О R,Если
q < 0, тоСвойства степеней: ![]()
Свойства 1 - 5 справедливы для всех действительных
a и b , при которых определены левые и правые части выписанных равенств, в частности, для любых a > 0, b > 0, a,b О R , свойство 6 - " указанных a,b ОR.Доказательства.
1. Пусть ![]() , где
, где
2. 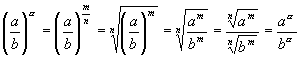
3.Свойства 3 и 4 вытекают из свойств корней 8 и определения степени: пусть ![]()
![]()
4. ![]()
5. ![]()
![]() ,
,
аналогично доказывается, что ![]()
6.![]() , m,n О N
, в силу только что доказанного свойства 5 и свойства 10 числовых неравенств
, m,n О N
, в силу только что доказанного свойства 5 и свойства 10 числовых неравенств ![]()
![]() ,
,
![]() , по доказанному и в силу свойства 9 числовых неравенств
, по доказанному и в силу свойства 9 числовых неравенств
![]()
Свойства степеней доказаны.