Учебник по Математике и Алгебре.

Оглавление учебника

АЛГЕБРА: Числа

2.1. Натуральные числа. Признаки делимости

Запись натуральных чисел.

Числа 1, 2, 3, 4, 5, …, использующиеся при счете предметов или для указания порядкового номера того или иного предмета среди однородных предметов называются натуральными. Любое натуральное число в десятичной системе счисления записывается с помощью цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Например, запись 2459 означает, что 2 - цифра тысяч, 4 - цифра сотен, 5 - цифра десятков, 9 - цифра единиц, т. е. 2459=2Ч 1000 + 4Ч 100 + 5Ч 10 + 9.

Вообще если а - цифра тысяч, b - цифра сотен, c - цифра десятков, d - цифра единиц, то имеем aЧ 1000+ +bЧ 100 + cЧ 10 + d. Используется также сокращенная запись . Аналогично запись означает число aЧ 10 000 + bЧ 1000 + cЧ 100 + dЧ 10 + e, причем a № 0.

Арифметические действия над натуральными числами.

Результатом сложения или умножения двух натуральных чисел всегда является натуральное число: если m и n - натуральные числа, то p = m + n тоже натуральное число, m, n - слагаемые, р - сумма; p=mn тоже натуральное число, m, n - множители, p - произведение.

Справедливы следующие свойства сложения и умножения натуральных чисел:

1° . a + b = b + a (переместительный закон сложения).

2° . (a + b) + c = a + (b + c) (сочетательный закон сложения).

3° . ab = ba (переместительное свойство умножения).

4° . (ab) c = a (bc) (сочетательное свойство умножения).

5° . a(b +c) = ab +ac (распределительное свойство умножения относительно сложения).

В результате вычитания или деления натуральных чисел не всегда получается натуральное число: например, 5 - 3 = 2 - натуральное число, тогда как 3 - 5 = -2 - не натуральное число; 18 : 6 = 3 - натуральное число, тогда как 15 : 2 = 5,5 - не натуральное число.

Если m, n, k - натуральные числа, то при m - n = k говорят, что m - уменьшаемое, n - вычитаемое, k - разность; при m : n =k говорят, что m - делимое, n - делитель, k - частное, число m называют также кратным числа n, а число n - делителем числа m. Если m, n О N , то m = np +r, где 0r< n. Если m - кратное числа n (m n), то r =0;

Из чисел с помощью знаков арифметических действий и скобок составляются числовые выражения. Если в числовом выражении выполнить указанные действия, соблюдая принятый порядок, то получится число, которое называется значением выражения.

Напомним порядок арифметических действий в числовом выражении: сначала выполняются действия в скобках; внутри любых скобок сначала выполняется умножение и деление, а потом сложение и вычитание. Например, в данном выражении порядок действия такой:

Признаки делимости.

Теорема 1 (теорема о делимости суммы).

Если каждое слагаемое делится на некоторое число, то и сумма делится на это число.

Доказательство:

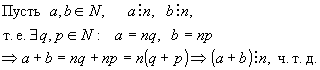
Теорема 2 (теорема о делимости произведения).

Если в произведении хотя бы один из множителей делится на некоторое число, то и произведение делится на это число.

Доказательство:

Рассмотрим для двух множителей (для большего числа аналогично).

 

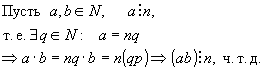
Пусть дано натуральное число ,

где

Пусть

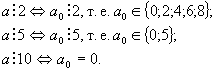
Пусть

Представим число a в таком виде

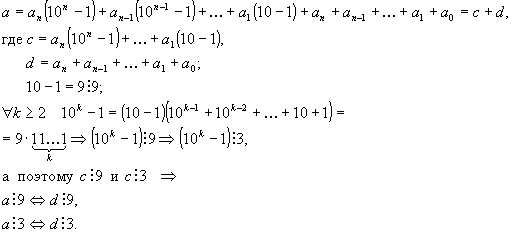
Итак,

Теорема 3 (признак делимости на 2).

Натуральное число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2.

Теорема 4 (признак делимости на 3).

Натуральное число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.

Теорема 5 (признак делимости на 4).

Натуральное число делится на 4 тогда и только тогда, когда делится на 4 двузначное число, образованное последними двумя цифрами данного числа.

Теорема 6 (признак делимости на 5).

Натуральное число делится на 5 тогда и только тогда, когда его последняя цифра либо 0, либо 5.

Теорема 7 (признак делимости на 9).

Натуральное число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Теорема 8 (признак делимости на 10).

Натуральное число делится на 10 тогда и только тогда, когда его последняя цифра 0.

Разложение простого числа на простые множители.

Натуральное число называется простым, если оно имеет только два делителя (само себя и единицу).

Натуральное число называется составным, если оно имеет более двух делителей.

Например, число 23 простое: 23 = 1Ч 23, а число 45 - составное, т. к. оно имеет 4 делителя:1, 5, 9, 45 и его можно представить в виде произведения больше, чем одним способом: 45 = 1Ч 45 = 5Ч 9.

Теорема 9.

Любое составное натуральное число можно разложить на простые множители и только одним способом.

При разложении чисел на простые множители используют признаки делимости. Если в разложении числа на простые множители один и тот же множитель встречается n раз, то записывают коротко: , т. е. Выражение называют степенью, - основанием степени, - показателем степени. Например, число 360 раскладывается так: 360 = 2Ч 2Ч 2Ч 3Ч 3Ч 5 =

Наибольший общий делитель нескольких натуральных чисел (Н.О.Д.).

Пусть даны числа a и b. Найдем все их делители. Среди делителей есть одинаковые, их называют общими делителями чисел a и b, а наибольшее среди них - наибольшим общим делителем. Обозначается Н.О.Д.(a;b). Если Н.О.Д.(a;b) = 1, то числа a и b называются взаимно простыми.

Чтобы найти наибольший общий делитель нескольких чисел, надо разложить эти числа на простые множители и найти произведение общих простых множителей, взяв каждый из них с наименьшим показателем.

П р и м е р. Найти Н.О.Д.(48, 60, 72).

Р е ш е н и е : 48 = ; 60 = ; 72 = . Значит, Н.О.Д.(48, 60, 72) = .

О т в е т: Н.О.Д.(48, 60, 72) =12.

Наименьшее общее кратное нескольких натуральных чисел (Н.О.К.).

Пусть даны числа a и b. Найдем числа, кратные им. Среди кратных есть одинаковые, их называют общими кратными чисел a и b, а наименьшее среди них - наименьшим общим кратным. Обозначается Н.О.К.(a;b). Любое общее кратное чисел a и b делится на Н.О.К.(a;b).

Чтобы найти наименьшее общее кратное нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим показателем.

П р и м е р. Найти Н.О.К.(48, 45).

Р е ш е н и е : 48 = ; 45 =. Значит, Н.О.К.(48, 45) = .

О т в е т: Н.О.К.(48, 45) =720.

Для любых натуральных a и b справедливо равенство

Н.О.Д.(a;b)Ч Н.О.К.(a;b) = ab.

В частности, если a и b взаимно простые, т. е. Н.О.Д.(a;b) = 1, то Н.О.К.(a;b) = ab. Это значит, что наименьшее общее кратное двух взаимно простых чисел равно произведению этих чисел.